Poornima
Saturday, 26 December 2020
Friday, 25 December 2020
Grade 10 Circles @2
Circles
1. PT is a tangent to the circle at T. If ![]() ; calculate:
; calculate:
i) ![]()
ii) ![]()
iii) ![]()
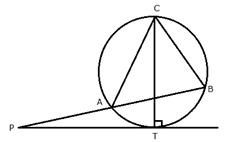
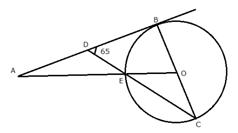
2. In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.
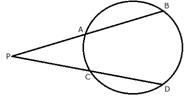
3.In the given figure, 3 x CP = PD = 9 cm and AP = 4.5 cm. Find BP.

4. In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4cm. Find CD.
5. In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4cm. Find CD.

6.n the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find
(i) AB.
(ii) the length of tangent PT.
7.In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ![]() ; calculate:
; calculate:
i) ![]()
ii) ![]()
iii) ![]()
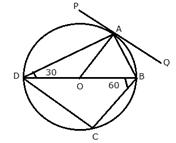
8.If PQ is a tangent to the circle at R; calculate:
i) ![]()
ii) ![]()

Given: O is the centre of the circle and ![]()
9. AB is diameter and AC is a chord of a circle with centre O such that angle BAC=30º. The tangent to the circle at C intersects AB produced in D. Show that BC = BD.
10.In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ![]() Find
Find ![]()
Tuesday, 22 December 2020
Grade 10 Circles @1
CIRCLES
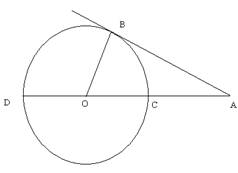
3.
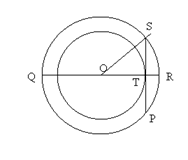
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
AP + BQ + CR = BP + CQ + AR.
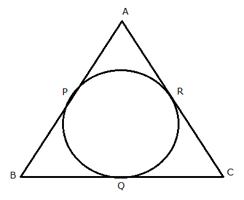
Also, show that AP + BQ + CR = ![]() x perimeter of triangle ABC.
x perimeter of triangle ABC.
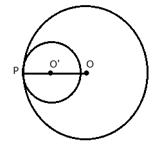
5.Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if -
i) they touch each other externally.
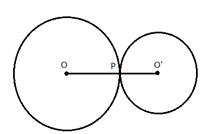
ii) they touch each other internally.
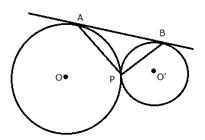
i) tangent at point P bisects AB.
ii) Angle APB = 90°
7.Two parallel tangents of a circle meet a third tangent at point P and Q. Prove that PQ subtends a right angle at the centre.
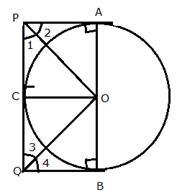

Calculate the value of x, the radius of the inscribed circle.
9.
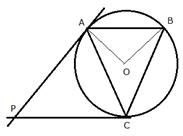
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i) ![]()
ii) ![]()
given that ![]()
10. In the following figure, PQ and PR are tangents to the circle, with centre O. If ![]() , calculate:
, calculate:
i) ![]()
ii) ![]()
iii)![]()













