Grade 10 Circles @2

 Circles

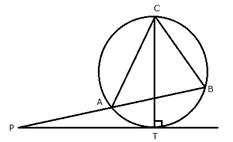
1. PT is a tangent to the circle at T. If ; calculate:

i) 

ii) 

iii) 

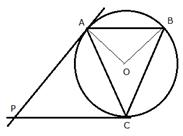
2. In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

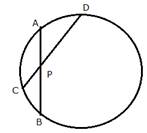
3.In the given figure, 3 x CP = PD = 9 cm and AP = 4.5 cm. Find BP.

4. In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4cm. Find CD.

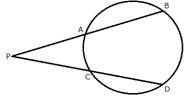
5. In the given figure, 5 x PA = 3 x AB = 30 cm and PC = 4cm. Find CD.

6.n the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find

(i) AB.

(ii) the length of tangent PT.

 

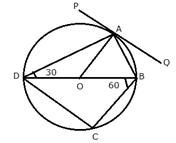
7.In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ; calculate:

i) 

ii) 

iii) 

8.If PQ is a tangent to the circle at R; calculate:

i) 

ii) 

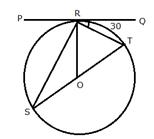
Given: O is the centre of the circle and 

9. AB is diameter and AC is a chord of a circle with centre O such that angle BAC=30º. The tangent to the circle at C intersects AB produced in D. Show that BC = BD.

10.In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B.  Find 

ANSWERS